請想想一個問題，大家都說戴安全帽比不戴安全帽安全，從邏輯上推論似乎沒錯，但從數字上，這似乎是根據事故發生率來判斷的。
譬如說，一百輛車，五十個人戴安全帽，其中戴安全帽的五十人有20人失事，不戴安全帽的有30人，那麼失事率當然是不戴安全帽高。但是，若這個城市大家都十分配合，100個人都戴上安全帽，難道就不會出車禍嗎？對，還是會，這時候戴安全帽的失事率就變成了…100%。戴安全帽的失事率是100%這樣暸嗎。

許多數字都只是表面上，藉由數字可以達成錯覺，也可增加可信度，是許多政客、演辯家常用的手法。

人看到很大的數字，就會一味的認為是絕對的大(這裡指的是非相對的絕對)，舉個例子，太陽和地球的距離是1ua，看似沒什麼，換成光要走500秒，這也還好，因為我們不是光無法理解，149597870691公尺，這個數字可能就會讓人頭暈目眩了。所謂的小，也是相同的道理，宇宙多大，垮克多小，都是不真實的數字。

123456789012345678901234567890123456789012345678901234567898123456789012345678901234567890
看似只是很正常的1~10，事實上其中有一組是1234567898，這是某種錯覺…
類似的道理可以做出許多詐欺術…

—980718
在《詭辯術》一書中第45節「統計法」，看到相同概念，得到印證。

這是一場矛盾的詭辯賽。
要進行論證，請先了解，若要證明一件事是對的，需要有條理的分析證明，但若要證明一件事是錯的，只要舉出一個反例即可。要說是規定也可，習慣也行，公理也通，反正就是如此。

「世界上沒有不可能」、「凡事都有例外」是兩個主角。

證明世界上沒有不可能：先假設世界上沒有不可能為真，那麼也就是世界上有可能有不可能，但是因為凡事都有例外，所以世界上沒有不可能也有例外，也就是世界上沒有不可能的例外就是世界上其實有不可能，而不可能的就是世界上不可能找到不可能，因此證明世界上沒有不可能。
若要證明凡事都有例外，請用反證法。假設凡事都沒有例外，那麼世界上沒有不可能也沒有例外，因此世界上絕對沒有不可能，也就是世界上絕對有可能找到不可能，這與世界上沒有不可能矛盾，因次得到結論凡事都有例外。

—980721 補充：
其實這段「解釋」還是有缺陷，也可以說是不合理之處，或是說是有漏洞，但不怎麼期望有人看的出來，意思就是「激將」希望有人可以看出來並且提出或反駁或一起來想想如何讓解釋更加完整。

—981115 更新：
在9~12樓的回應中已提到上文所說的缺陷，留待各位細心發掘，並期待可以獲取一些建設性的意見以使此缺陷掩蓋或有任何更完美證法歡迎提出。

請先看看這篇故事，時空旅行的矛盾。
—
一九四五年，一位來路不明的女嬰被棄置在克里夫蘭的一所孤兒院。
「珍」在孤獨和落寞中長大，不知道她的親生父母是誰，直到一九六三年的某日，她莫名其妙地愛上一位流浪漢。正當珍的際遇開始好轉時，災禍卻接踵而至。
她懷了流浪漢的孩子，流浪漢卻不見蹤影。
在複雜的生產手術中，醫生赫然發現珍有兩套性器官。
為了拯救珍的生命，他們只好為珍進行變性手術，讓「她」變成「他」。
最後，一位神秘的陌生人，從產房中綁走了她的孩子。

經歷了這些打擊，被社會排斥，被命運嘲笑的「他」，變成了一位酒鬼和流浪漢。
珍不但失去了雙親和愛人，連自己的孩子也失去了。到了一九七０年，他走進冷清的「老爹酒吧」，向一位老酒保說出他悲哀的一生。
酒保答應幫他報復對「她」始亂終棄的陌生人，條件是他必須參加「時間旅行團」。
他們兩人進入時間機器，酒保將流浪漢留在一九六三年。
流浪漢莫名其妙地愛上一位年輕的孤兒，後來讓她懷孕了。

酒保繼續前進九個月，從醫院綁走女嬰，將女嬰棄置於一九四五年的一所孤兒院。
後來酒保將流浪漢帶到一九八五年，成為「時間旅行團」的一員。
流浪漢終於開始過著穩定的生活，成為「時間旅行團」中一位受人尊敬的老會員。
後來他化身為一位酒保，接下最棘手的任務：和命運的約會，
在一九七０年的「老爹酒館」和一位流浪漢碰面。
—
很明顯，這篇故事充滿了疑點。
首先這篇的來源已經不明，我試著要找出原文，但是似乎是某小說的翻譯，在這邊就不追究了。

再看一次，或許就會明白，故事中所有主角都是同一人，而造成混亂的就是「時間旅行」，所有人物的父母也都是自己本身，再來請看看這張圖。
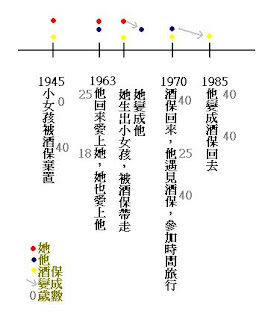這樣很好理解，事實上所有主角與主角之間的接觸只是自己不同年紀時的接觸罷了。
這個故事同時也表達了無限和零的概念，因為這可以無限的循環下去，也是從無中生有，小女孩從哪來的？是長大後的她自己生出來的，小女孩的父親則是母親的未來，而酒保又扮演了製造與解釋疑點的角色。

當然要找出疑點也不是那麼容易，試想，酒保在棄置小女孩後應該是又回到了1970，在1985被年輕的自己給取代，年輕的酒保又回到過去準備製造出另一個新的自己，那麼若這個故事持續的循環下去，不是就會有許多的老酒保出現。當然這還不足以推翻這個故事。

酒保為何要帶走小女孩？在動機的部份也沒辦法解釋，故事中也沒有交代清楚，或許只是為了讓故事完整。這也不足以推翻。

再來看看各人物的起始與終點，「她」是被「她」生出來的，最後變成「他」，「他」是由「她」變來的，最後變成「酒保」，「酒保」是由「他」變來的，最後不清楚。
因為已經討論過酒保的結局並不會對故事造成影響，因此要推翻這個故事必定要從「她是被她生出來的」著手。
從年齡來說0歲的她被18歲的她(與25歲的他)生出來，在這一瞬間(若酒保也剛好出現，他也還在)事實上是存在四個同質不同年紀的人。

但是這樣看下來，這個故事好像也沒有地方可以推翻？不合理的地方有很多但是都不足以推翻掉。難道這是可能發生的嗎？

有人知道的話麻煩透漏一下，謝謝。

—980806
出處：Robert A. Heinlein《行屍走肉》-摘要（All You Zombies…），

—980806 23:05
為了找出這篇的疑點，我找遍了許多地方，再一個小小的網誌找到了一篇故事，帶給我很大的啟發，因此我認為，人類是無法改變歷史的，請看這篇，「時空旅行無法改變歷史」，這也解釋了這篇的矛盾之處了，同時得到印證。

辯題：「大雄需要/不需要小叮噹」。
賽制：奧瑞岡三三三制。

壹、首先，名詞解釋：
時空悖論：又稱「祖父悖論」簡單白話解釋為你不能回到過去殺掉自己的祖父，詳見後參考處。
宿命論：命運無法被改變是早已決定好的，基本上與時空悖論相近。

貳、「反方」(不需要)詭辯術
利用時間軸及時空悖論加上宿命論的概念



勝。

叁、「正方」辯論稿，’表對方反駁 ”表反駁對方反駁

1.作者定義觀點：
藤子·F·不二雄已經將大雄定義為需要哆啦A夢的人，而哆啦A夢即為被需要者。
若大雄不需要哆啦A夢則哆啦A夢就沒有存在的意義，因為哆啦A夢的出現本來就是為了被需要，作者為了使漫畫完整而製造出哆啦A夢這個角色被大雄需要。
根據維基百科「哆啦A夢角色列表」中哆啦A夢的定義中提到「為了改變大雄命運而來。」
「哆啦A夢百科」提到其正式的職業名稱為「特定意志薄弱兒童監視指導員」，所以其實大雄就是所謂「意志薄弱兒童」，而這也證明了哆啦A夢是為了大雄而存在。

‘ 無法證明作者定義。
” 若作者定義出其他與原意義不同的定義，則此部片哆啦A夢就沒有存在價值，且在哆啦A夢角色列表中的定義已經提到是為了改變大雄命運而來的，換言之，哆啦A夢是因大雄而存在。

2.根據結局與需要之定義：
定義”需要”，根據「教育部重編國語辭典修訂本」需要的定義為：
1.必須。(不夠完整)
2.心理學上指當個體感受缺乏時所產生的內在心理狀態。包括生理上的需要，如飢、渴，以及心理上的需要，如孤獨、寂寞。(生理+心理) (以此為憑)
3.經濟學上指在一定時間、一定市場，依一定價格而獲得滿足的商品量。對商品不僅能購買，而且願意購買。(經濟學無關)

再補充更完整：任一時刻產生需要即為需要。(任何一瞬間而非所有時間)

根據維基百科中「哆啦A夢最終回」中的三種正式版結局，有一種結局不完整且有矛盾故不討論，其中兩種共同點皆為大雄並不希望哆啦A夢離開，因此確定大雄其實是需要哆啦A夢的，這也符合需要的定義。
又根據需要的定義，再最後一集中確定大雄產生需要哆啦A夢，所以可以推論大雄需要哆啦A夢成立。

‘ 引用「哆啦A夢最終回」中，「有三個正式版本，但皆隨著連載劇情的發展而轉為非正式結局。」
「後來作者去世前表明《哆啦A夢》沒有實質上結局，並隨著過世而結束連載，現今仍以動畫的形式延續《哆啦A夢》的故事。」

3.時空悖論：
哆啦A夢由未來回到過去，因兩人有相遇並共同生活，所以時間軸產生重疊，也就是同一條時間軸，因此若少了哆啦A夢則此時間軸消失，所以證明大雄是需要哆啦A夢來完成未來的。(此情況特殊，在此宿命論與時空悖論相牴觸)

‘ 宿命論，大雄並不需要哆啦A夢來完成未來，因為歷史並不會改變，可能會產生其他替代方案來取代哆啦A夢，兩條時間軸互不相干，就算失去哆啦A夢這條時間軸也不會影響到大雄的時間軸的發展。

” 故事中可改變歷史，根據某集，大雄坐時光機到未來製作出化石，証明在故事中歷史是可改變的，故宿命論在劇情中並不成立。

肆、必不敗之詭辯術之題目缺陷之鑽牛角尖：(注意：為”必不敗”而非”必勝”)
1976年小叮噹遇見大雄
1997小叮噹改名為哆啦A某夢
2123小叮噹誕生

事實上，1997年後所畫的動畫都已稱作哆啦A夢因此與辯題「大雄需不需要”小叮噹”」不符，故所有提出論點有引用到動畫及電影情節者皆稱為無根據。

伍、恐怖資料之參考文獻
維基百科：
哆啦A夢
哆啦A夢道具列表
哆啦A夢角色列表
哆啦A夢最終回
2112年哆啦A夢的誕生
哆啦A夢 (漫畫角色)
哆啦A夢百科
藤子不二雄
祖父悖論
時間旅行
宿命論

哆啦A夢結局資料
哆啦A夢改名資料
2008/02/08 「大型強子對撞機」將在日內瓦啟用 相關新聞

請自行觀賞。

因 若p則q與若非q則非p等價，因此若「生前不必多睡」則「死後自然長眠」與若「死後不會長眠」則「生前必須多睡」等價。
但因大前提：「死後不會長眠」唯一未知，而在證明上無法以未知的理論作為論證來辯駁，因此無法成立。
因此得到命題『若「死後不會長眠」則「生前必須多睡」』為假命題，得到『若「生前不必多睡」則「死後自然長眠」』為假。

因此得到最重要的結果：盡量睡吧各位。