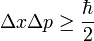這是一篇看起來就很唬爛的學術性文章,裡面竟然在嘗試同時用古典力學[1]和量子力學[2]解釋一個人類根本就無法理解的狀況。
在這裡我要先做出聲明,這並不是普通艱深與普通唬爛程度的文章,裡面也並沒有使用詭辯、沒有融入任何悖論,並且會消耗大多數的腦細胞,如果想要完全看懂並提出反駁請先理解內文中提到的許多原理及理論,在文末會附上註解提供外連,定義部分以及計算過程也會盡可能的附在文末,建議想看懂本文的人要先確定自身已經瞭解文內提到的細節。
首先,直接進入本文的題目:如果有一顆球,從高處落下,與地面碰撞反彈後又落下反彈如此往復進行,它會不會停?單看此題目敘述十分簡顯易懂,但是現在要開始做出比題目還長的補充:假設此小球非常小,在此以一原子來做替代,但為了理解方便後文還是以球代稱。地面質量十分龐大,在此以地球來做替代,不考慮空氣阻力,直接去掉大氣層的存在。但是並不忽略所有其他的因素及外力。
現在要討論的是,這顆球到底「會不會停」?先考慮現實生活中,無論多麼大力丟球,球都會停下來,我們可以理解這是因為空氣阻力的存在,加上地球質量遠大於小球的質量造成。但是現在沒有了空氣阻力,我必須先解釋本文考慮的因素非常細微,提出一個極端的例子:如果兩個無氫鍵[3]的原子在無外力的狀況下相互因萬有引力接近後又因電子的靜電力彈開,如此重複,會呈現簡諧運動[4]並永遠不會停止,而兩原子的平衡點便是斥力與引力相等的位置。
回到文中的狀況,為什麼地球與小球就不會進行這樣的簡諧運動了呢?其實還是會的,只是質量相差太過懸殊,振幅太過微小無法觀察,但是,在文中還是不會忽略此種狀況。
看過以上例子後相信各位可以理解這是不會停止的簡諧運動,但是回到此段第一句的問題,也就是這顆球永遠不會停?這時候必須再引入量子力學中的「震盪[5]」,在大部分科學家的眼中,所謂的「靜止」基本上就是不考慮原子在原地做微小的震盪,換句話說,原子在原地做微小的震盪還是可以算是靜止的。
這時候各位大概可以了解我要表達的是什麼,在這裡我把「靜止」的定義做出不包括震盪的補充。直接切入原題後也就是這顆球「會停」,而且根據定義是在彈起的高度(振幅)不大於震盪的振幅時稱做「停」。
但是這時候又產生了一個問題,這個簡諧運動為什麼又會停了呢?根據剛剛的敘述這應該是個永遠不會停止的簡諧運動,在這裡我要提醒各位再度回到巨觀的世界中,兩物體簡諧運動的振幅通常是在「振幅小於兩物平衡點距離」下做討論的吧,因為在巨觀世界中振幅不能大於兩者的距離,否則那便是碰撞的情況而不是簡諧運動了。因此再回到原子的世界中,這個簡諧運動的前提也就是振幅要夠小才行。
文章至此終於定義告一段落,並解釋完部份的原理。
撰稿至此,赫然發現「震盪」其實就是量子力學中的「共振」,但經過確定後兩者可以通用。
這時候如果要進入題目的計算,想必必須要先得知震盪的振幅,才能算出在什麼時候此反彈才會停止,但是若要算出共振的振幅,可以透過一個與線性震盪器類似的公式[6]求得,但是這又會牽扯入兩個反彈的原子的特性,包括公式內所需要的的衰變率(Γ)及質量(竟是以複數M+iΓ的形式來做計算)。
所以在這邊直接再引入「測不準原理[7]」,測不準原理並不只是在「測」中出現,而是物質本身就具無法確定的不確定性,所以也稱為「不確定性原理」,因此本題中雖不考慮觀測者及觀測方法的因素,仍然可以適用此原理。
根據測不準原理直接導出的結論,如果物體運動的位置變化如果在小於約化蒲朗克常數[8]的一半時,這便是沒有意義的(或說做無法觀測的),所以我們可以直接做出結論:振幅小於蒲朗克常數的一半時便是靜止。
現在終於可以進入原題目的計算,以下自行假設實際狀況。
假設小球是一個碳(12C)[9]原子,質量為12amu=1.992646632*10-26kg,初落下高度為1公里,反彈的恢復係數[10]是e=0.5,也就是碰撞後的速率變為碰撞前的一半,計算後得到彈起的高度會是落下高度的1/4。
速度變化為:1st落下末速為140m/s,2nd落下末速為一半70m/s…類推。
第n次落下末速為140/2n-1。
落下高度變化:1st落下1000m,2nd落下250,3rd落下125/2,4th落下125/8…類推。
故:1000∞Σn=0 1/(4n),當然不會是無限而是暫用這個符號來表示,這是個收斂的級數,每項會趨近於0,第n項為1000/4n-1。
設第n項動量與位置的乘積小於約化蒲朗克常數的一半(5.272858409*10-35),代入公式[11]得到n>17.6(計算過程[12]),意即第17次彈跳後停止。
令人驚訝的是,這時候的速度還有0.159cm/s,而高度有58207.66皮米[13](碳原子半徑為67皮米),即已經「測不準」了。
(此段與本文只有少許關聯)在這邊順道計算一些其他東西彈跳的n值,先把算式整理成公式後:n>LOG10(16*M*H*SQRT(2*9.8*H)/h)/(3*LOG10(2)),(可直接複製至excel用,M=質量(kg),H=高度(m),h=約化蒲朗克常數)。
可以得到有趣的數字:
–>
|
質量M
|
落下高度H
|
n最小整數值
|
|
1公克
|
1公分
|
35
|
|
1公斤
|
1公尺
|
42
|
|
1公噸
|
1公里
|
50
|
|
地球質量
|
地球半徑
|
80
|
|
太陽質量
|
1AU
|
94
|
–>
(當然了,後面兩項並不是帶入公式這麼單純的,純屬趣味。)
計算的部分先告一段落,現在進入無限的領域,理論上來講,雖然我們定義他停了,但是它可能還會繼續不斷的細微運動(或是共振),所以這跳到了另一個問題:到底要多久才會停?現在只考慮牛頓力學的部分,根據力學能守恆我們可以計算出第n次的反彈速度為en(2gh)1/2,第n次反彈後在空中停留的時間為2en(2h/g)1/2,總時間為T=(2h/g)1/2(1+2∞Σn=1en)=(1+e/1-e)(2h/g)1/2,e為恢復係數 (計算[14])。
所以現在根據前文討論的結果,總時間為T,但是我們知道落下的高度會逐漸趨近於0,但卻永遠不會為0→所以它永遠不會停,因為永遠可以落下。
再回到純數學的部分,剛剛算出的T時是總時間,因此我們知道第k+1次會比第k次的時候更接近T,第k+2次也會比第k+1次的時候更接近T…類推,此級數會不斷逼近T卻永遠不會到達,這十分類似於阿基里斯與烏龜賽跑的悖論[15]。
這時候回到現實,如果我們坐著時光機直接跳到T時去,看到的到底會是什麼呢?
很明顯,這是一個無窮級數的不可靠之處,根據公式可以求出一個確切的數值,但其實也可以說這數值並不存在或沒有意義。
要破解這道謎題,就必須再往回看,把前文提到的測不準原理一併應用進去,這便是為什麼這是同一篇文章的理由。
根據古典力學、牛頓力學→它會永遠運動。
根據測不準原理、量子力學→它會停。
根據無窮數列、無窮級數→它不會停,但可以求總時間逼近值。
「→」表示根據…得到。
這些東西單獨看都不好理解,但大家卻習以為常;合再一起看不可置信,卻又合乎邏輯,因為定義各自不完整,但合在一起後卻可以相互補充。
至於如果你要問我關於無窮的問題,我會說「人的理解是有限的,所以無法探討無限的問題」來帶過,雖然敷衍,但是這才是最正確的解釋。
註釋:
[1] 古典力學:以牛頓運動定律為基礎,在巨觀世界和低速狀態下,研究物體運動的基要學術。
[2] 量子力學:描寫微觀物質的一個物理學理論,與相對論一起被認為是現代物理學的兩大基本支柱,許多物理學理論和科學如原子物理學、固體物理學、核物理學和粒子物理學以及其它相關的學科都是以量子力學為基礎。
[3] 氫鍵:是分子間作用力(凡得瓦力)的一種,是一種永久偶極之間的作用力。
[4] 簡諧運動:進行簡諧運動時,物體所受的力跟位移成正比,並且力總是指向平衡位置。
[5] 共振:量子力學與量子場論中,共振可能出現在與古典物理相似的場合。
[6]  Γ是粒子衰變率,而Ω由粒子質量M取代,頻率為ω。
Γ是粒子衰變率,而Ω由粒子質量M取代,頻率為ω。
[7] 測不準原理:指在一個量子力學系統中,一個粒子的位置和它的動量不可被同時確定。
[9] 碳:非金屬元素,位於元素周期表的第二周期IVA族。它的化學符號是C,它的原子序數是6,電子構型為[He]2s22p2。
[10] 恢復係數:兩個物體在碰撞時,恢復期與形變期的衝量的比率稱為恢復係數。
[11] 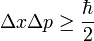 。
。
[12] 質量以M表示,約化蒲朗克常數的一半以h’表示,則:
M*(19600/2n-1)*( 1000/4n-1)>=h’ (移項並整理)
→23n>(1.568*108*m)/h’ (同取log2後除以3)
→n>log(1.568*108*m/h’)/3log2
代入原式m及h後得到n>18.5726。
[13] 皮米:皮米(picometer或pm)是長度單位,1皮米相當於1米的一兆(即一萬億)分之一。有時在原子物理學中稱為微微米(micromicron)
[14] 第一次與地面接觸時的速度 v0=(2gh)1/2
第一次反彈速度 v1=ev0
第二次反彈速度 v2=ev1
第n次反彈速度vn=evn-1 vn=evn-1=e2vn-2=…=env0=en(2gh)1/2
第n次觸地後停留空中時間 tn=2vn/g=en(2h/g)1/2
總時間 T= (2h/g)1/2(1+2∞Σn=1en)=(1+e/1-e)(2h/g)1/2。
[15] 阿奇里斯悖論:動得最慢的物體不會被動得最快的物體追上。由於追趕者首先應該達到被追者出發之點,此時被追者已經往前走了一段距離。因此被追者總是在追趕者前面。
本文題目及[14]解法來自:《1994~2009年國際物理奧林匹亞競賽國家代表隊選拔考試 初選試題及解答彙編》,p.36第十題。
有關無窮級數的某小部分想法來自:《毛起來說三角》,Eli Maor,湖守仁譯,天下遠見出版股份有限公司。
在此感謝我的暑假作業。
另外,本文構思、撰稿、查資料、複審、校稿共花了至少七個小時,感謝您閱讀至此,歡迎提出批評及修正。